Hands-On Equations Research
Research Highlights
Studies in more than 135 classrooms in 17 states involving more than 2,500 students have yielded unequivocal evidence of the ability of elementary and middle school students to quickly learn basic algebraic concepts through the use of the Hands-On Equations method of instruction and to transfer their learning to the pictorial representation.
Research Highlights
Click here to view the listing of available research reports.
Excerpts from Published Papers
“The findings suggest that the seven-lesson Hands-On Equations Level I instructional program offers a promising approach to significantly impact LD students, effectively bridging the initial achievement gap in solving linear equations and raising their scores to the post-test level of the non-LD students. The design of the Hands-On Equations manipulatives and the accompanying instruction appears to have facilitated an understanding of the relational meaning of the equal sign, symbolic algebraic notation, and methods for simplifying and solving equations, including those with the unknown on both sides, and those that otherwise would require the knowledge of the distributive property” (p. 34)
Borenson, H. (2025). An effective algebra intervention for teaching linear equations to middle school students with learning disabilities. https://doi.org/10.31235/osf.io/h9ueg_v1 (Preprint)
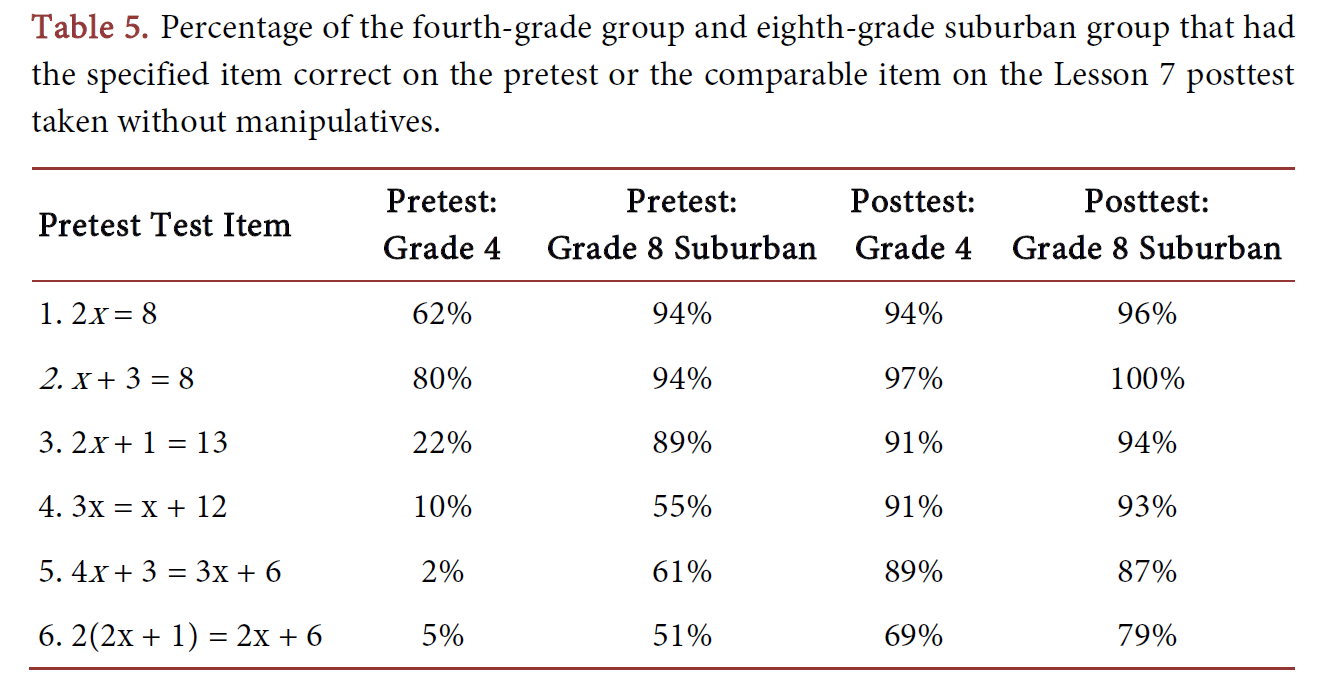
“The results showed that eighth graders outperformed fourth graders on the benchmark pretest. However, after seven lessons using this balance model, the fourth graders showed a statistically significant gain of three standard deviations, outperforming the eighth-grade pretest scores. The model helped the younger students to make sense of formal algebraic notation, the relational meaning of the equal sign, and the subtraction property of equality, which are essential concepts for future algebraic studies. The study also found a statistically significant gain in the eighth graders’ performance with a moderate effect size. Therefore, upper elementary and middle school students should use this algebra balance model to enhance their equation-solving ability” (p. 1600).
Borenson, H. (2023). The Hands-On Equations balance model enhances algebraic equation solving in upper elementary and middle school students. Creative Education, 14, 1600-1620. https://doi.org/10.4236/ce.2023.148104
“Based on our findings, we suggest mathematics teachers endeavor to use Hands-On Equations materials and pictorial representations to help students develop a conceptual basis for translating and solving word problems involving linear equations with one unknown.” (Page 12)
Tackie, N.A, Sheppard, P., and Flint, T.K. (2018). “Engendering algebraic readiness through pictorial representations”, Investigations in Mathematics Learning” (April 2018), pp. 1 – 13. Research Council on Mathematical Learning.
“After the class interventions, all teachers regarded their physical manipulative group lesson as the most successful. They reasoned that the physical manipulative provided students with a concrete and tactile learning experience and also facilitated students’ individual and group languaging. In their opinion, when physically handling the manipulative, students concretely constructed conceptual understanding of: 1) equation equivalence through the balance scale; 2) constants and variables through their distinct representations (number cubes and pawns); and 3) performing the same operation on both sides of the equation through actual action of removing the same elements from both sides of the balance scale. Thus, the physical manipulative groups had a better understanding of equation concepts compared to the other groups.” (Page 178)
“It is important to realize that no content is developmentally appropriate or inappropriate in and of itself…During the development of algebraic understanding, the learner moves from concrete to abstract thinking. Henry Borenson’s work with fourth graders, who according to cognitive stage theory are generally expected to be in the concrete operational stage, shows that they are able to transition to abstract thinking if they initially experience algebraic principles using concrete manipulatives along with symbolic representations (Borenson & Barber, 2008). An effective instructional strategy begins with transforming the word problem into a concrete or pictorial equation. When the learner becomes proficient with creating and interpreting concrete representations of equations, the teacher can demonstrate how to use that representation to construct an abstract equation using a letter for the unknown. The concrete representation can be used as long as the learner requires the structure, which may be different lengths of time for different students.” (Pages 18 – 19)
Morrissey, C., Boula, J. and Morgan, K. (2017). Application of the Deans for Impact Report, The Science of Learning How Do Students Understand New Ideas? Journal of Applied Educational and Policy Research, 3(1).
“…moving from concrete to abstract thinking is key to understanding algebra, with which many students struggle, particularly at younger ages, when they theoretically are in Piaget’s concrete operational stage. However, Henry Borenson’s work with young children using his Hands-On Equations program (available as a series of apps as well as in physical individual and classroom-scale programs) demonstrates that if children experience algebraic principles using concrete strategies initially, then the transition to abstract thinking can occur at younger ages (Borenson and Barber 2008)” (Page 38).
Walling, Donovan (2014). “Developing Activities that Match Learner Needs” in Designing Learning for Tablet Classrooms: Innovation in Instruction, pp. 37-42. Springer International Publishing.
“By first teaching the concept of equivalence nonsymbolically, using the balance model or using concrete objects, and only afterward relating that learning to the symbolic notation, we can provide young students with a successful introduction to the relational meaning of the equal sign.” (Page 94)
Borenson, Henry (2013). “A Balancing Act” Teaching Children Mathematics. Vol. 20, No. 2 (September 2013), pp. 90-94. National Council of Teachers of Mathematics.
“By using this approach, proceeding from the concrete to the abstract, U.S. students can exceed their age/grade counterparts in high achieving countries on this goal (of representing multistep word problems using a letter for the unknown).” (Page 25)
Borenson, Henry (2012). ” Are the common core state standards for mathematics in grades three and four reasonable? Rethinking word problems using a letter for the unknown. “ Newsletter of the National Council of Supervisors of Mathematics (NCSM), Volume 42, Number 4, 24-25.
“The students easily appropriated the manipulative material, starting to solve intuitively simple and fairly complex equations.” (Page 2)
Silvestre, A. I., Nunes, C., & Jacinto, H. (2012) LESSON STUDY APPROACH TO THE TEACHING OF LINEAR EQUATIONS: A PORTUGUESE CASE OF TEACHERS’PROFESSIONAL DEVELOPMENT.
“Hands-On Equations is an algebraic learning environment in the sense that students are often able to develop some abstract concepts on their own.” (Page 27)
Borenson, Henry (2011). “Demystifying the Learning of Algebra Using Clear Language, Visual Icons, and Gestures.” Newsletter of the National Council of Supervisors of Mathematics (NCSM), Volume 41, No, (3): 24-27.
“Experience with nonsymbolic equivalence problems can actually lead to improvements on subsequent symbolic problems.” (Page 97)
Sherman, Jody and Jeffrey Bisanz (2009). “Equivalence in symbolic and nonsymbolic contexts: benefits of solving problems with manipulatives.” Journal of Educational Psychology, Volume 101, No. 1, 88 – 100. American Psychological Association.
“In the physical environment, students could pick up and move the algebra pieces easily without the use of a mouse. Their movements were more efficient with the algebra pieces. Because the algebra pieces were more open-ended and did not provide students with a guided process for solving the equations, this encouraged some students to invent their own strategies for solving equations, rather than following a traditional algorithm…The open-ended feature of Hands-On Equations also prompted students to use more mental mathematics in their calculations and allowed them to process numerical relationships mentally before writing down their ideas.” (Page 164)
Suh, J., & Moyer, P. S. (2007). Developing students’ representational fluency using virtual and physical algebra balances. The Journal of Computers in Mathematics and Science Teaching, 26(2), 155.
“Our results show that the balance model is especially suited to the study of how to solve equations. In fact, the isomorphism between the object itself and the mathematical notions implied allows students to form a mental image of the operations that they have to apply. They are able to reactivate this self-evident image at any moment.” (Page 355)
Vlassis, Joelle (2002). “The balance model: hindrance or support for the solving of linear equations with one variable.” Educational Studies in Mathematics 49, 341-359. Netherlands: Kluwer Academic Publishers.
“I want ALL my students to discover math for themselves, and Hands-On Equations does this. It guides them to a higher and more sophisticated level of mathematical thinking and understanding.” (Page 299)
Raymond, Anne M. and Leinenbach, Marylin (2000). “Collaborative action research on the learning and teaching of algebra: a story of one mathematics teacher’s development.” Educational Studies in Mathematics 41, 283-287. Netherlands: Kluwer Academic Publishers.
“100% of the students demonstrated at least 80% mastery on at least two out of the three tests that followed the instruction. Students that qualify for special education assistance and at-risk remedial instruction, as well as learning different students and attention deficit hyperactive students, performed as well as those in regular education without those classifications.” (Page 36)
Barclay, Jennifer (1992). A study of a manipulative approach to teaching linear equations to sixth-grade students. Unpublished master’s thesis. Texas Woman’s University, Denton, TX.
“These children are not only able to solve correctly these ninth-grade algebraic linear equations, they are also able to verbalize what they are doing and the logic behind it. In other words, through these concrete experiences, the children are developing a sound mathematical sense about algebraic linear equations and how they work.” (Page 55)
Borenson, Henry (1987). “Algebra for gifted third graders.” Gifted Child Today, Volume 10, No. 3, 54-56. GCT, Inc.